![[PukiWiki]](image/logo_state-senri3_80x80.png "[PukiWiki]"){kind=logo}
vdW-DFの使い方 †概要 †van der Waals密度汎関数(vdW-DF)法では交換相関項は以下で与えられます。 \[ E_{\rm xc}=E_{\rm x}^{\rm GGA}+E_{\rm c}^{\rm LDA}+E_{\rm c}^{\rm NL} \]
GGAとの大きな違いは、相関項が局所部分\( E_{\rm c}^{\rm LDA} \)と非局所部分 \[ E_{\rm c}^{\rm NL}=\int{\rm d}\bm{r}{\rm d}\bm{r}'\rho(\bm{r})\phi\bigl(q_0(\bm{r})R,q_0(\bm{r}')R\bigr)\rho(\bm{r}'),\qquad R\equiv|\bm{r}-\bm{r}'| \]
からなる点です。 \( E_{\rm x}^{\rm GGA} \)と\( E_{\rm c}^{\rm NL} \)の汎関数形には任意性があるため、それらの組み合わせにより以下の様なvdW-DFが提案されています。
交換汎関数の違いに関しては交換増強因子を参照。 計算例: グラファイト †入力ファイル †0 0 0 0 0 0 : graphite 8.00 20.00 1 4 4 : GMAX, GMAXP, NTYP, NATM, NATM2 1 0 : num_space_group, type of bravis lattice 4.663851051 4.663851051 10.000000000 90.0 90.0 60.0 : a,b,c,alpha,beta,gamma ............ (1) 24 24 2 1 1 1 : knx,kny,knz, k-point shift 0 0 : NCORD, NINV 0.000000000000 0.000000000000 0.250000000000 1 1 1 0.333333333333 0.333333333333 0.250000000000 1 1 1 0.000000000000 0.000000000000 -0.250000000000 1 1 1 -0.333333333333 -0.333333333333 -0.250000000000 1 1 1 6 0.1500 1.00794 3 1 0.d0 : TYPE 1IATOMN,ALFA,AMION,ILOC,IVAN 0 0 0 0 0 : ICOND 0-MD, 1-CONT.MD, 2-WAVE FN,, 3-WAVE FN CONT., iconstpw 0 1 : IPRE, IPRI 200 1000 0 57200.00 0 : NMD1, NMD2, iter_last, CPUMAX,ifstop 6 1 : Simple=1,Broyd2=3,Blugel=6, 1:charge, 2:potential mix. 0 30 0.5 : starting mixing, kbxmix,alpha 0.60 0.50 0.60 0.70 1.00 : DTIM1, DTIM2, DTIM3, DTIM4, dtim_last 100.00 2 1 0.10D-08 1.d-06 : DTIO ,IMDALG, IEXPL, EDELTA -0.0010 1.00D+03 0 : WIDTH,FORCCR,ISTRESS vdw-df 1 : XCTYPE, nspin .......................................... (2) 1.00 3 : destm, n_stm 101 : NBZTYP 0-SF, 1-BK, 2-SC, 3-BCC, 4-FCC, 5-DIA, 6-HEX 0 0 0 : NKX, NKY, NKZ 0 0 0 : NKX2,NKY2,NKZ2 12 : NEG 1 : NEXTST(MB) 0 : 0; random numbers, 1; matrix diagon 2 0 0 0(MB) : imsd, i_2lm, i_sd2another, wksz for phase 0 : evaluation of eko difference.0 = no ,1 = yes 0 : npdosao 0 0.0 : SM_N, dopping (1) 面内の格子定数は単層グラフェンで各汎関数に対して得られた値を採用。 (2) XCTYPEに上表で与えられた汎関数のキーワードを選択 計算結果 †ノルム保存型擬ポテンシャル(pbe6TM)を使用。 $ grep ETOT nfout_1|grep "[0-9]" ETOT: 1 7.32313472 0.7323E+01 0.4287E-01 ETOT: 2 -7.60683998 0.1493E+02 0.1266E-01 ETOT: 3 -14.03669542 0.6430E+01 0.1740E-01 ETOT: 4 -18.03943434 0.4003E+01 0.2143E-01 ETOT: 5 -21.11405447 0.3075E+01 0.2687E-01 ETOT: 6 -22.87848370 0.1764E+01 0.2967E-01 ETOT: 7 -23.16877237 0.2903E+00 0.3184E-01 ETOT: 8 -23.18140643 0.1263E-01 0.3211E-01 ETOT: 9 -23.06892067 0.1125E+00 0.4670E-01 ETOT: 10 -23.05209913 0.1682E-01 0.4879E-01 ETOT: 11 -23.05837868 0.6280E-02 0.4928E-01 ETOT: 12 -22.96174397 0.9663E-01 0.6045E-01 ETOT: 13 -22.95306285 0.8681E-02 0.6154E-01 ETOT: 14 -22.95134524 0.1718E-02 0.6176E-01 ETOT: 15 -22.94584745 0.5498E-02 0.6260E-01 ETOT: 16 -22.90587940 0.3997E-01 0.6946E-01 ETOT: 17 -22.90870079 0.2821E-02 0.6914E-01 ETOT: 18 -22.93237537 0.2367E-01 0.6522E-01 ETOT: 19 -22.95150617 0.1913E-01 0.6250E-01 ETOT: 20 -23.02433643 0.7283E-01 0.5876E-01 ETOT: 21 -23.20830145 0.1840E+00 0.3174E-01 ETOT: 22 -23.26514139 0.5684E-01 0.1768E-01 ETOT: 23 -23.23630949 0.2883E-01 0.2640E-01 ETOT: 24 -23.23617609 0.1334E-03 0.2614E-01 ETOT: 25 -23.23088093 0.5295E-02 0.2754E-01 ETOT: 26 -23.23666860 0.5788E-02 0.2557E-01 ETOT: 27 -23.23902197 0.2353E-02 0.2470E-01 ETOT: 28 -23.23834303 0.6789E-03 0.2491E-01 ETOT: 29 -23.23402514 0.4318E-02 0.2517E-01 ETOT: 30 -23.24644645 0.1242E-01 0.2132E-01 ETOT: 31 -23.24804788 0.1601E-02 0.2078E-01 ETOT: 32 -23.28102960 0.3298E-01 0.1090E-01 ETOT: 33 -23.28989968 0.8870E-02 0.2136E-02 ETOT: 34 -23.29000192 0.1022E-03 0.9084E-03 ETOT: 35 -23.29002861 0.2668E-04 0.1287E-03 ETOT: 36 -23.29003080 0.2193E-05 0.4038E-04 ETOT: 37 -23.29003099 0.1909E-06 0.1070E-04 ETOT: 38 -23.29003097 0.2252E-07 0.1287E-05 ETOT: 39 -23.29003097 0.6872E-09 0.5571E-06 ETOT: 40 -23.29003097 0.8149E-09 0.9540E-07 ETOT: 41 -23.29003097 0.4122E-09 0.3396E-07 ETOT(Q) + SM_energy = -23.2900309657897 0.000000000000000E+000 層間相互作用エネルギー †孤立したgrapheneの計算も行い \[ E_{\rm int}=E_{\rm graphite}-2E_{\rm graphene} \]
から層間の相互作用エネルギーを求める。 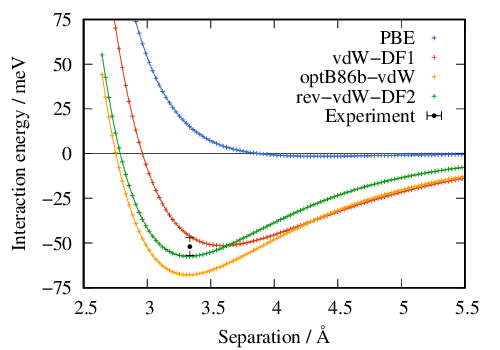 オプション †Self-consistent vdW-DF法で用いる2つのパラメータのデフォルト値は以下の通り(STATE 5.6.0以降)。
これらを変更する場合には入力ファイルの下部に &VDW-DF qcut 値 nqs 値 &END のような記述を追加。 注意 †STATE 5.5.4でのデフォルト値はqcut=3.d0, nqs=10となっていましたので、STATE 5.6.0以降と比較するときは明示的にqcutとnqsを指定する必要があります。 |
Last-modified: 2023-01-23 (月) 11:57:01 (464d)