Crystalline aluminum †
This tutorial explains how to perform the convergence study with respect to the number of k-points and smearing width, and how to analyze the electronic structure, i.e., band structure and density of states.
Convergence study †
Metallic systems have the Fermi surface, and to handle it, STATE uses the smearing technique with various smearing functions and the tetrahedron method.
Furthermore, the number of k-points to sample the Brillouin zone can be critical for the accurate calculation of the metallic systems.
Convergence with respect to the number of k-points †
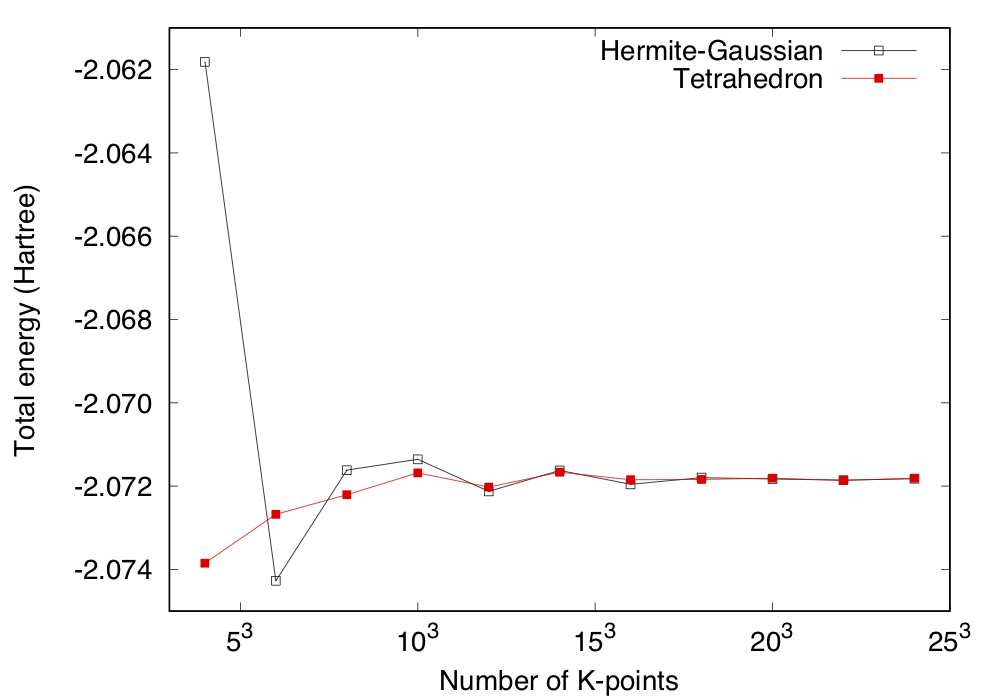
Here we present the convergence of the total energy with respect to the number of k-points with the Methefeesel-Paxton smearing (default) and tetrahedron methods.
Use negative WIDTH (e.g. -0.02) to activate the Methefessel-Paxton smearing (with positive value, a parabolic function is used to treat the Fermi level and the entropic term is not taken into account).
- Input file for the smearing method
0 0 0 0 0 0 : I_CTRL(1:6) (DUMMY)
4.00 8.00 1 1 1 : GMAX GMAXP NTYP NATM NATM2
221 2 : NUM_SPACE_GROUP TYPE
7.5967 7.5967 7.5967 90.0 90.0 90.0 : A B C ALPHA BETA GAMMA
06 06 06 1 1 1 : N1 N2 N3 M1 M2 M3
0 0 : NCORD, NINV
0.00 0.00 0.00 1 0 1 : CPS(1,1:3) IWEI IMDTYP ITYP
13 0.50 26.98 6 1 0.2 : IATOMN ALFA AMION ILOC IVAN
0 0 0 0 0 : ICOND INIPOS INIVEL ININOS INIACC
0 1 : IPRE IPRI
30 30 0 84200.00 0 : NMD1 NMD2 LAST_ITER CPUMAX IFSTOP
6 1 : WAY_MIX MIX_WHAT
0 20 0.60 : ITER_START KBXMIX MIX_ALPHA
0.20 0.30 0.20 0.20 0.20 : DTIM1 DTIM2 DTIM3 DTIM4 DTIM
300.00 4 1 0.50D-09 : DTIO IMDALG IEXPL EDELTA
-0.0020 0.50D+03 0 : WIDTH FORCCR ISTRESS
ggapbe 1 : XCTYPE KSPIN
2.00 : DESTM
101 : NBZTYPE
4 4 4 : NKX NKY NKZ (DUMMY)
4 4 4 : NKX2 NKY2 NKZ2 (DUMMY)
6 : KEG
1 : NEXTST
0 : (DUMMY)
2 : IMSD
0 : EVALUATE_EKO_DIFF
0 : NPDOSAO
0 0.000 : SM_N DOPPING (DUMMY)
- Input file for the tetrahedron method
0 0 0 0 0 0 : I_CTRL(1:6) (DUMMY)
4.00 8.00 1 1 1 : GMAX GMAXP NTYP NATM NATM2
221 2 : NUM_SPACE_GROUP TYPE
7.5967 7.5967 7.5967 90.0 90.0 90.0 : A B C ALPHA BETA GAMMA
06 06 06 1 1 1 : N1 N2 N3 M1 M2 M3
0 0 : NCORD, NINV
0.00 0.00 0.00 1 0 1 : CPS(1,1:3) IWEI IMDTYP ITYP
13 0.50 26.98 6 1 0.2 : IATOMN ALFA AMION ILOC IVAN
0 0 0 0 0 : ICOND INIPOS INIVEL ININOS INIACC
0 1 : IPRE IPRI
30 30 0 84200.00 0 : NMD1 NMD2 LAST_ITER CPUMAX IFSTOP
6 1 : WAY_MIX MIX_WHAT
0 20 0.60 : ITER_START KBXMIX MIX_ALPHA
0.20 0.30 0.20 0.20 0.20 : DTIM1 DTIM2 DTIM3 DTIM4 DTIM
300.00 4 1 0.50D-09 : DTIO IMDALG IEXPL EDELTA
-10.02 0 0.50D+03 0 : WIDTH FORCCR ISTRESS
ggapbe 1 : XCTYPE KSPIN
2.00 : DESTM
101 : NBZTYPE
4 4 4 : NKX NKY NKZ (DUMMY)
4 4 4 : NKX2 NKY2 NKZ2 (DUMMY)
6 : KEG
1 : NEXTST
0 : (DUMMY)
2 : IMSD
0 : EVALUATE_EKO_DIFF
0 : NPDOSAO
0 0.000 : SM_N DOPPING (DUMMY)
See the difference in WIDTH.
By calculating the total energy as a funciton of the number k-ponts, we obtain the following:
Convergence with respect to the smearing width †
Total (free) energy of the metallic system is sensitive to the smearing width, in particular, with the Gaussian and Fermi-Dirac function. Here we demonstrate the smearing width dependence of the total energy, following the seminal work by de Gironcoli [Phys. Rev. B51, 6773(R) (1995)].
Smearing function can be chosen by adding the section &OTHERS ... &END at the end of the input file. To use the Fermi-Dirac distribution function set
&OTHERS
FERMI_DIRAC
&END
For the Gaussian smearing
&OTHERS
GAUSSIAN
&END
The cold smearing of Marzari and Vanderbilt is also available. Use
&OTHERS
COLD
&END
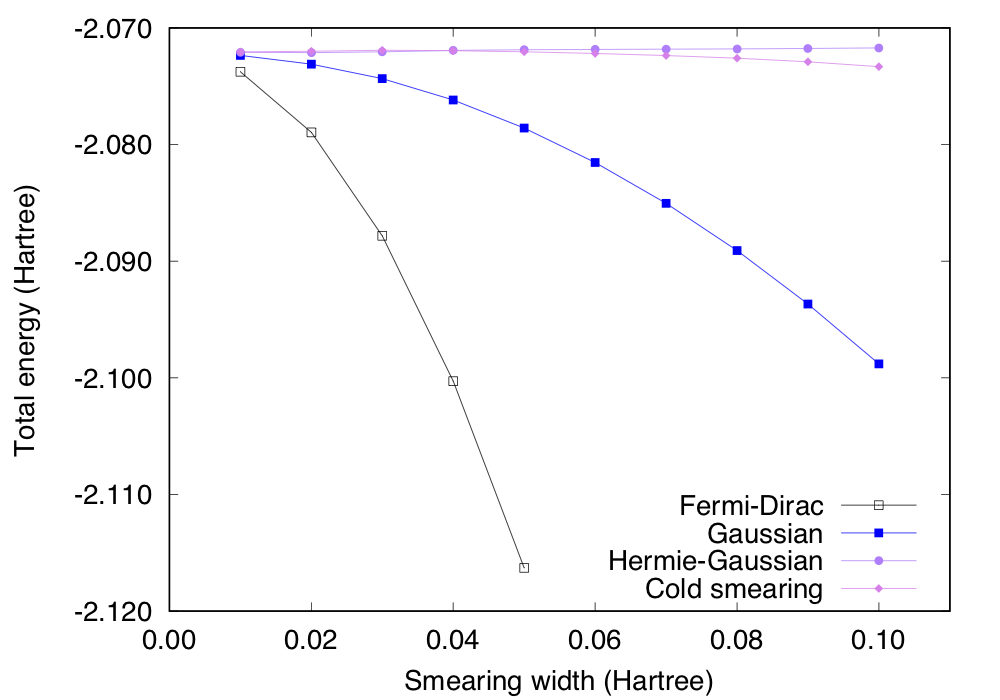
By calculating the total energy as a function of smearing width using different smearing function, we obtain the following
We can see that the total energy depends significantly on the smearing width with Fermi-Dirac and Gaussian, whereas the total energy is not sensitive to the width with Hermite-Gaussian and cold smearing.
Band structure calculation †
Let us dicuss how to perform the band structure analysis.
First of all, we need to get electron density and perform a self-consistent-field (SCF) calculation. Below is an example of the input file for the SCF calculation with relatively coarse k-point grid.
- Input file (nfinp_scf)
0 0 0 0 0 0 : I_CTRL(1:6) (DUMMY)
4.00 8.00 1 1 1 : GMAX GMAXP NTYP NATM NATM2
221 2 : NUM_SPACE_GROUP TYPE
7.5967 7.5967 7.5967 90.0 90.0 90.0 : A B C ALPHA BETA GAMMA
06 06 06 1 1 1 : N1 N2 N3 M1 M2 M3
0 0 : NCORD, NINV
0.00 0.00 0.00 1 0 1 : CPS(1,1:3) IWEI IMDTYP ITYP
13 0.50 26.98 6 1 0.2 : IATOMN ALFA AMION ILOC IVAN
0 0 0 0 0 : ICOND INIPOS INIVEL ININOS INIACC
0 1 : IPRE IPRI
30 30 0 84200.00 0 : NMD1 NMD2 LAST_ITER CPUMAX IFSTOP
6 1 : WAY_MIX MIX_WHAT
0 20 0.60 : ITER_START KBXMIX MIX_ALPHA
0.20 0.30 0.20 0.20 0.20 : DTIM1 DTIM2 DTIM3 DTIM4 DTIM
300.00 4 1 0.50D-09 : DTIO IMDALG IEXPL EDELTA
-0.0020 0.50D+03 0 : WIDTH FORCCR ISTRESS
ggapbe 1 : XCTYPE KSPIN
2.00 : DESTM
101 : NBZTYPE
4 4 4 : NKX NKY NKZ (DUMMY)
4 4 4 : NKX2 NKY2 NKZ2 (DUMMY)
6 : KEG
1 : NEXTST
0 : (DUMMY)
2 : IMSD
0 : EVALUATE_EKO_DIFF
0 : NPDOSAO
0 0.000 : SM_N DOPPING (DUMMY)
Then we perform a non-self-consisnten-filed (non-SCF) calculation using the converged electron density. Specifically we solve the Kohn-Sham equation along the high symmetry lines in the Brillouin zone. Below is an example for the non-SCF band structure calculation.
- Input file (nfinp_band)
0 0 0 0 0 0 : I_CTRL(1:6) (DUMMY)
4.00 8.00 1 1 1 : GMAX GMAXP NTYP NATM NATM2
221 2 : NUM_SPACE_GROUP TYPE
7.5967 7.5967 7.5967 90.0 90.0 90.0 : A B C ALPHA BETA GAMMA
06 06 06 1 1 1 : N1 N2 N3 M1 M2 M3
0 0 : NCORD, NINV
0.00 0.00 0.00 1 0 1 : CPS(1,1:3) IWEI IMDTYP ITYP
13 0.50 26.98 6 1 0.2 : IATOMN ALFA AMION ILOC IVAN
22 0 0 0 0 : ICOND INIPOS INIVEL ININOS INIACC
0 1 : IPRE IPRI
30 30 0 84200.00 0 : NMD1 NMD2 LAST_ITER CPUMAX IFSTOP
6 1 : WAY_MIX MIX_WHAT
0 20 0.60 : ITER_START KBXMIX MIX_ALPHA
0.20 0.30 0.20 0.20 0.20 : DTIM1 DTIM2 DTIM3 DTIM4 DTIM
300.00 4 1 0.50D-09 : DTIO IMDALG IEXPL EDELTA
-0.0020 0.50D+03 0 : WIDTH FORCCR ISTRESS
ggapbe 1 : XCTYPE KSPIN
2.00 : DESTM
101 : NBZTYPE
4 4 4 : NKX NKY NKZ (DUMMY)
4 4 4 : NKX2 NKY2 NKZ2 (DUMMY)
6 : KEG
1 : NEXTST
0 : (DUMMY)
2 : IMSD
0 : EVALUATE_EKO_DIFF
0 : NPDOSAO
0 0.000 : SM_N DOPPING (DUMMY)
&KPOINTS_BAND
NKSEG 4
KMESH 40 20 20 20
KPOINTS
0.000 0.000 0.000
0.000 0.500 0.500
0.250 0.500 0.750
0.500 0.500 0.500
0.000 0.000 0.000
&END
To perform the band structure, ICOND must be set to 22 as
22 0 0 0 0 : ICOND INIPOS INIVEL ININOS INIACC
In addition, the (high-symmetry) k-points, which define the symmetry, should be given in the &KPOINTS_BAND ... &END block.
&KPOINTS_BAND
NKSEG 4
KMESH 40 20 20 20
KPOINTS
0.000 0.000 0.000
0.000 0.500 0.500
0.250 0.500 0.750
0.500 0.500 0.500
0.000 0.000 0.000
&END
Here
NKSEG
is the number of k-point segments. The k-point mesh for each segment follows
KMESH
and k-points in the reduced coordinate are given below
KPOINTS
The number of k-points should be NKSEG+1.
When the non-SCF band structure is finished, the eigenvalues are printed in "energy.data", which cannot be plotted directly.
To plot the band structure, the "energy2band" program is provided.
Just execute
> energy2band
and provide the number of bands in the calculation, the number of bands to be plotted, the number of total k-points in the non-SCF band structure calculation, and the Fermi level in Hartree, as prompted, "band.data" is created.
The "band.data" can be used to plot the band structure by using for e.g., gnuplot and xmgrace. Here's an example of gnuplot script:
set terminal postscript eps 'Helvetica' 22
set output 'band.eps'
emin=-12.5
emax=12.5
xmin=0.0
xmax=2.54176932
G=0.0
X=0.82709404
W=1.24064106
L=1.82548487
G2=2.54176932
offset=0.75
set xrange [xmin:xmax]
set yrange [emin:emax]
unset key
unset xtics
unset xlabel
set ylabel 'E-E_F (eV)'
set xzeroaxis
set arrow from X,emin to X,emax nohead
set arrow from W,emin to W,emax nohead
set arrow from L,emin to L,emax nohead
set label '{/Symbol G}' at G,emin-offset center
set label 'X' at X,emin-offset center
set label 'W' at W,emin-offset center
set label 'L' at L,emin-offset center
set label '{/Symbol G}' at G2,emin-offset center
plot 'band.data' using 1:2 with lines lw 3
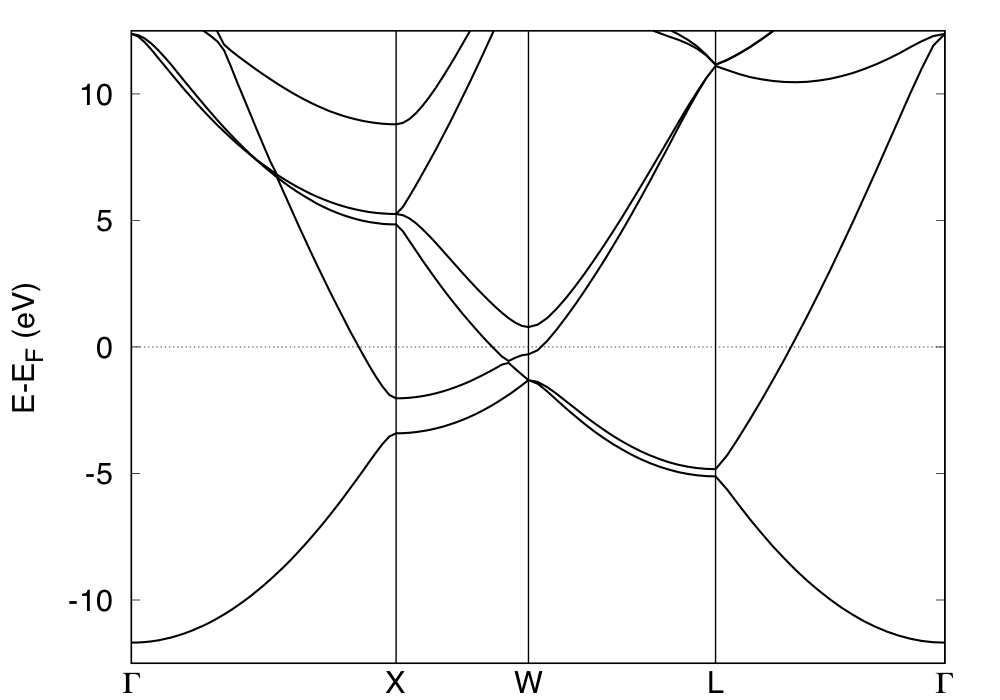
and by using this script one may get the following:
Excersie †
- Perform convergence study of lattice parameter to see the impact of the number of k-points and smearing width. Further compare the equilibrium lattice parameters obtained using the smearing and tetrahedron methods.
![[PukiWiki] [PukiWiki]](image/logo_state-senri3_80x80.png)