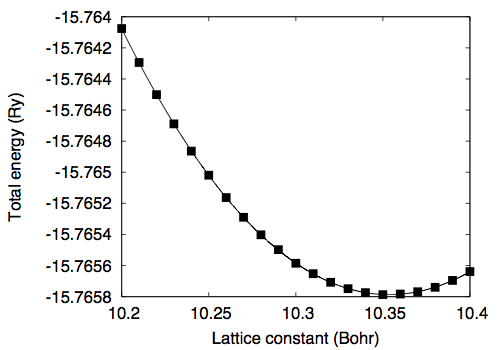
Silicon in the diamond structure †In this tutorial how to optimize the cell parameter(s) of a crystal is described by using Silicon in the diamond structure as an example. Optimization of cell parameters (1) †As a way of optimizing the cell parameter of crystalline Silicon, let us calculate the total energy as a function of cell parameter a (celldm(1) or alat) by using the following input file. &control calculation='scf' restart_mode='from_scratch', pseudo_dir = '/home/ikutaro/QE/pseudo/', outdir='./tmp' prefix='si' tstress = .true. tprnfor = .true. nstep = 500 verbosity='high' / &system ibrav = 2 celldm(1) = 10.35 nat = 2 ntyp = 1 ecutwfc = 35.0 / &electrons diagonalization='cg' conv_thr = 1.0e-12 mixing_beta = 0.7 / ATOMIC_SPECIES Si 0.000 Si_ONCV_PBE-1.1.upf ATOMIC_POSITIONS (crystal) Si 0.0000 0.0000 0.0000 Si 0.2500 0.2500 0.2500 K_POINTS (automatic) 04 04 04 1 1 1 Here the cutoff energy of 35 Ry and the shifted (Monkhorst-Pack) k-point mesh of 4 x 4 x 4 are used. By varying the lattice parameter (celldm(1)) from 10.20 to 10.40, the following data is obtained 10.20 -15.76407573 10.21 -15.76429413 10.22 -15.76450080 10.23 -15.76468908 10.24 -15.76486394 10.25 -15.76501895 10.26 -15.76516290 10.27 -15.76528971 10.28 -15.76540192 10.29 -15.76549787 10.30 -15.76558501 10.31 -15.76565239 10.32 -15.76570775 10.33 -15.76574875 10.34 -15.76577425 10.35 -15.76578726 10.36 -15.76578313 10.37 -15.76576812 10.38 -15.76573973 10.39 -15.76569547 10.40 -15.76563892 By fitting the total energy to the 6th order polynomial, equilibrium lattice constant of 10.3536 Bohr (5.4789 Angstrom) is obtained. Optimization of cell parameters (2) †In the case of crystalline silicon, the manual optimization (i.e. calculation of the total energy as a function of cell parameter) is straightforward. However, if the system has a more complicated structure with low symmetry, the manual optimization is too complicated. In such a case we are able to calculate the stress tensor and optimize the cell parameters in addition to the internal coordinates. Here's how to optimize the cell parameter: The input file looks like: &control calculation = 'vc-relax' restart_mode = 'from_scratch', pseudo_dir = '/home/ikutaro/QE/pseudo/', outdir = './tmp' prefix = 'si' tstress = .true. tprnfor = .true. forc_conv_thr = 2.0d-4 / &system ibrav = 2 celldm(1) = 10.20 nat= 2 ntyp= 1, ecutwfc = 35.0 / &electrons diagonalization = 'cg' conv_thr = 1.0e-12 mixing_beta = 0.7 / &ions / &cell press = 0.0d0 press_conv_thr = 0.5d0 cell_dynamics = 'bfgs' & ATOMIC_SPECIES Si 0.000 Si_ONCV_PBE-1.1.upf ATOMIC_POSITIONS (crystal) Si 0.0000 0.0000 0.0000 Si 0.2500 0.2500 0.2500 K_POINTS (automatic) 04 04 04 1 1 1 In the cell optimization, the following is used calculation = 'vc-relax' where "vc" stands for "variable cell shape." In addition, the following name lists should be included in the input file &ions / &cell press = 0.0d0 press_conv_thr = 0.5d0 cell_dynamics = 'bfgs' & See the input description for more options. When "tstress = .true." the stress tensor and pressur are printed as Computing stress (Cartesian axis) and pressure
total stress (Ry/bohr**3) (kbar) P= 42.13
0.00028636 0.00000000 0.00000000 42.13 0.00 0.00
-0.00000000 0.00028636 0.00000000 -0.00 42.13 0.00
0.00000000 0.00000000 0.00028636 0.00 0.00 42.13
When the cell optimization converges, the cell parameters, as well as the atomic positions are printed in the output as Begin final coordinates
new unit-cell volume = 277.12964 a.u.^3 ( 41.06638 Ang^3 )
density = 2.27130 g/cm^3
CELL_PARAMETERS (alat= 10.20000000)
-0.507322537 -0.000000000 0.507322537
0.000000000 0.507322537 0.507322537
-0.507322537 0.507322537 -0.000000000
ATOMIC_POSITIONS (crystal)
Si -0.000000000 0.000000000 -0.000000000
Si 0.250000000 0.250000000 0.250000000
End final coordinates
Note that the "CELL_PARAMETERS" should be multiplied with "alat" (in Bohr) to get the cell parameter (alat is fixed throughout the calculation and cell parameters scaled by alat are varied during the cell optimization). The lattice parameter obtained by the "vc-relax" is 10.3494 Bohr (5.4767 Angstrom), which is slightly different from that obtained by the manual optimization. Note that for the cell optimization with the stress, relatively large cutoff energy is required and care must be taken especially for the cutoff energy. Exercise †The cell parameters should be converged with respect to cutoff energy and k-point. When do the lattice parameters obtained by the manual optimization and automatic optimization coincide within the certain error? What is the smallest cutoff energy needed to perform the "accurate" calculation? |
![[PukiWiki] [PukiWiki]](image/logo_state-senri3_80x80.png)