Silicon in the diamond structure †

In this tutorial how to optimize the cell parameter(s) of a crystal is described by using Silicon in the diamond structure as an example.

↑

Optimization of cell parameters (1) †

As a way of optimizing the cell parameter of crystalline Silicon, let us calculate the total energy as a function of cell parameter a (celldm(1) or alat) by using the following input file.

&control
   calculation='scf'
   restart_mode='from_scratch',
   pseudo_dir = '/home/ikutaro/QE/pseudo/',
   outdir='./tmp'
   prefix='si'
   tstress = .true.
   tprnfor = .true.
   nstep = 500
   verbosity='high'
/
&system
   ibrav = 2, celldm(1) = 10.35, nat= 2, ntyp= 1,
   ecutwfc = 35.0
   !nbnd=48
   !occupations='smearing', smearing='mp', degauss=0.02
/
&electrons
   diagonalization='cg'
   conv_thr = 1.0e-12
   mixing_beta = 0.7
/
ATOMIC_SPECIES
 Si  0.000   Si_ONCV_PBE-1.1.upf
ATOMIC_POSITIONS (crystal)
 Si  0.0000  0.0000  0.0000
 Si  0.2500  0.2500  0.2500
K_POINTS (automatic)
 04 04 04 1 1 1

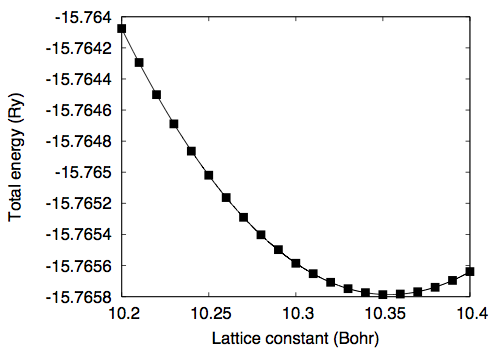
Here the cutoff energy of 35 Ry and the shifted (Monkhorst-Pack) k-point mesh of 4 x 4 x 4 are used. By varying the lattice parameter (celldm(1)) from 10.20 to 10.40, the following data is obtained

10.20 -15.76407573
10.21 -15.76429413
10.22 -15.76450080
10.23 -15.76468908
10.24 -15.76486394
10.25 -15.76501895
10.26 -15.76516290
10.27 -15.76528971
10.28 -15.76540192
10.29 -15.76549787
10.30 -15.76558501
10.31 -15.76565239
10.32 -15.76570775
10.33 -15.76574875
10.34 -15.76577425
10.35 -15.76578726
10.36 -15.76578313
10.37 -15.76576812
10.38 -15.76573973
10.39 -15.76569547
10.40 -15.76563892
ftot_Si.png

By fitting the total energy to the 6th order polynomial, equilibrium lattice constant of 10.3536 Bohr (5.4789 Angstrom) is obtained.

↑

Optimization of cell parameters (2) †

In the case of crystalline silicon, the manual optimization (i.e. calculation of the total energy as a function of cell parameter) is straightforward. However, if the system has a more complicated structure with low symmetry, the manual optimization is too complicated. In such a case we are able to calculate the stress tensor and optimize the cell parameters in addition to the internal coordinates. Here's how to optimize the cell parameter: The input file looks like:

&control
   calculation   = 'vc-relax'
   restart_mode  = 'from_scratch',
   pseudo_dir    = '/home/ikutaro/QE/pseudo/',
   outdir        = './tmp'
   prefix        = 'si'
   tstress       = .true.
   tprnfor       = .true.
   forc_conv_thr = 2.0d-4
/
&system
   ibrav     = 2
   celldm(1) = 10.20
   nat= 2
   ntyp= 1,
   ecutwfc = 35.0
/
&electrons
   diagonalization = 'cg'
   conv_thr        = 1.0e-12
   mixing_beta     = 0.7
/
&ions
/
&cell
   press          = 0.0d0
   press_conv_thr = 0.5d0
   cell_dynamics  = 'bfgs'
&
ATOMIC_SPECIES
 Si  0.000   Si_ONCV_PBE-1.1.upf
ATOMIC_POSITIONS (crystal)
 Si  0.0000  0.0000  0.0000
 Si  0.2500  0.2500  0.2500
K_POINTS (automatic)
 04 04 04 1 1 1

In the cell optimization, the following is used

   calculation   = 'vc-relax'

where "vc" stands for "variable cell shape." In addition, the following name lists should be included in the input file

&ions
/
&cell
   press          = 0.0d0
   press_conv_thr = 0.5d0
   cell_dynamics  = 'bfgs'
&

See the input description for more options. When "tstress = .true." the stress tensor and pressur are printed as

     Computing stress (Cartesian axis) and pressure

          total   stress  (Ry/bohr**3)                   (kbar)     P=   42.13
   0.00028636   0.00000000   0.00000000         42.13      0.00      0.00
  -0.00000000   0.00028636   0.00000000         -0.00     42.13      0.00
   0.00000000   0.00000000   0.00028636          0.00      0.00     42.13

When the cell optimization converges, the cell parameters, as well as the atomic positions are printed in the output as

Begin final coordinates
     new unit-cell volume =    277.12964 a.u.^3 (    41.06638 Ang^3 )
     density =      2.27130 g/cm^3

CELL_PARAMETERS (alat= 10.20000000)
  -0.507322537  -0.000000000   0.507322537
   0.000000000   0.507322537   0.507322537
  -0.507322537   0.507322537  -0.000000000

ATOMIC_POSITIONS (crystal)
Si      -0.000000000   0.000000000  -0.000000000
Si       0.250000000   0.250000000   0.250000000
End final coordinates

Note that the "CELL_PARAMETERS" should be multiplied with "alat" to get the cell parameter (alat is fixed throughout the calculation and cell parameters scaled by alat are varied during the cell optimization).

The lattice parameter obtained by the "vc-relax" is 10.3494 Bohr (5.4767 Angstrom), which is slightly different from that obtained by the manual optimization. Note that for the cell optimization with the stress, relatively large cutoff energy is required and care must be taken especially for the cutoff energy.

↑

Exercise †

The cell parameters should be converged with respect to cutoff energy and k-point. When do the lattice parameters obtained by the manual optimization and automatic optimization coincide within the certain error? What is the smallest cutoff energy needed to perform the "accurate" calculation?

トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS