Hydrogen molecule †

In this tutorial, how to execute pw.x and how to converge computational parameters, such as kinetic energy cutoff and box size are described by taking hydrogen molecule (H2) as an example. How to optimize the molecular geometry is also described.

In a standard plane-wave pseudopotential code, three-dimensional periodic boundary condition is employed, and an isolated molecule is modeled by placing it in a large box in such a way that the electrostatic interactions with neighboring images can be negligible. If the box is large enough, the Brillouin zone becomes small (as it scales as (2p/a)**3), thus the Brillouin zone is sampled only at the Gamma point [(0,0,0)]. In this case, the accuracy of the calculation is controlled by increasing the kinetic energy cutoff, which corresponds to increasing the real-space mesh (resolution of the wave function in real space) and by increasing the box size. The latter is to confirm that the interaction between image molecules is negligibly small and that the model mimics the molecule in its an isolated state.

↑

Preliminary †

↑

SCF calculation †

Let us begin with an SCF calculation of H2 having the experimental bond length of 0.74 Angstrom in a cubic box with the edges of 10 Angstrom. We use the SG15 optimized norm-conserving pseudopotentials with the cutoff energy of 30 Ry. The input file for this calculation is called "h2_scf.in" and is the following:

&control
   calculation   = 'scf'
   restart_mode  = 'from_scratch',
   pseudo_dir    =  '/home/ikutaro/QE/pseudo/'
   outdir        = './tmp/'
   prefix        = 'h2'
   tprnfor       = .true.
   forc_conv_thr = 1.d-4
/
&system
   ibrav   = 1
   A       = 10.d0
   nat     = 2
   ntyp    = 1
   nbnd    = 4
   ecutwfc = 30.0
   ecutrho = 120.0
/
&electrons
   diagonalization = 'david'
   conv_thr        = 1.0e-12
   mixing_beta     = 0.1
/
ATOMIC_SPECIES
 H 0.0000  H_ONCV_PBE-1.0.upf
ATOMIC_POSITIONS (angstrom)
H      0.000000000000      0.000000000000      0.00000000000
H      0.000000000000      0.000000000000      0.74000000000
K_POINTS (gamma)

Here the number of electron is 2 and thus the minimum number of bands is 1, but slightly large number of bands of 4 is used. Note "pseudo_dir" and "outdir" should be modified according to the environment. To perform the SCF calculation, we use pw.x. Here let us assume we are going to use pw.x in $HOME/QE/src/qe-6.2.1 and execute the following

$ mpirun -np 2 $HOME/QE/src/qe-6.2.1/bin/pw.x < h2_scf.in > h2_scf.out

or for the group's cluster execute

$ qsub h2.sh

where the job script "h2.sh" looks like

#$ -S /bin/bash
#$ -cwd
#$ -q xe1.q
#$ -pe x8 8
#$ -N H2
#
source /opt/setting/2016.4/intel-compiler.sh
source /opt/setting/2016.4/intel-mpi.sh
#
INPUT_FILE='h2_scf.in'
OUTPUT_FILE='h2_scf.out'
#
PW_DIR=/home/ikutaro/QE/src/qe-6.3/bin
#
MPI_COMMAND=mpirun
PW_COMMAND=pw.x
PW=$PW_DIR/$PW_COMMAND
#
I_MPI_PIN=1
I_MPI_FABRICS=shm:ofa
OMP_NUM_THREADS=1
#
cat $PE_HOSTFILE | awk '{ print $1":"$2/ENVIRON["OMP_NUM_THREADS"] }' > 
hostfile.$JOB_ID
# 
$MPI_COMMAND $PW < $INPUT_FILE > $OUTPUT_FILE

When the SCF convergence is archived, the following can be found in the output file (h2_scf.out).

!    total energy              =      -2.31431279 Ry
     Harris-Foulkes estimate   =      -2.31431279 Ry
     estimated scf accuracy    <          3.7E-13 Ry

     The total energy is the sum of the following terms:

     one-electron contribution =      -3.79278238 Ry
     hartree contribution      =       2.01958218 Ry
     xc contribution           =      -1.37197167 Ry
     ewald contribution        =       0.83085908 Ry

     convergence has been achieved in  15 iterations

If "tprnfor = .true." the following lines can also be found

     Forces acting on atoms (cartesian axes, Ry/au):

     atom    1 type  1   force =     0.00000000    0.00000000   -0.03012765
     atom    2 type  1   force =     0.00000000    0.00000000    0.03012765
↑

Convergence study †

↑

Convergence wrt cutoff †

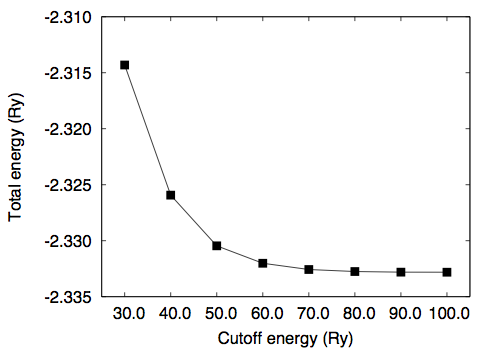
To study the convergence of the total energy, we calculate the total energy as a function of kinetic energy cutoff ("ecutwfc") by fixing the molecular structure. Note that in the present case normconserving pseudopotential is used and ecutrho is fixed to 4 times larger than ecutwfc (ecutrho = 4 * ecutwfc). Results are as follows

# ecutwfc (Ry) total energy (Ry)
  30.0         -2.31431279
  40.0         -2.32593152
  50.0         -2.33045981
  60.0         -2.33201780
  70.0         -2.33257560
  80.0         -2.33275476
  90.0         -2.33280832
  100.0        -2.33281717
ftot_H2_ecut.png
↑

Convergence wrt box size †

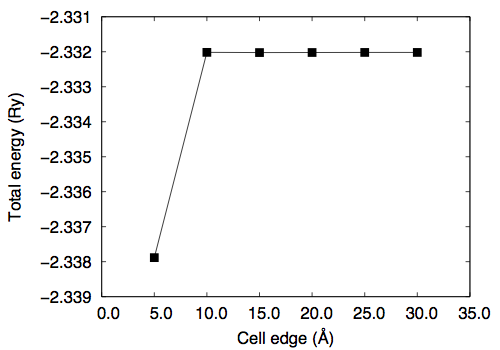
Then let us calculate the total energy as a function of the cell edge. In this study, ecutwfc=60.0 Ry is used.

# a (Angstrom) total energy (Ry)
5.0            -2.33788501
10.0           -2.33201780
15.0           -2.33202479
20.0           -2.33202183
25.0           -2.33202063
30.0           -2.33202053
ftot_H2_boxsize.png
↑

Optimizing the bond length (1) †

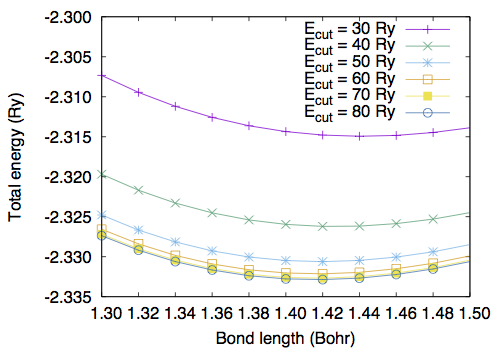
Let us determine the bond length of H2. First, we calculate the total energy as a function of bond length. The input files are the same as the one for the SCF calculation, but the position of the second H atom. We set the z-coordinate of the second H atom ranging from 1.3 to 1.5 Bohr. Here is the result with ecutwfc=60Ry :

1.30 -2.32657183
1.32 -2.32840377
1.34 -2.32984183
1.36 -2.33091143
1.38 -2.33163627
1.40 -2.33203866
1.42 -2.33213950
1.44 -2.33195843
1.46 -2.33151384
1.48 -2.33082299
1.50 -2.32990212

By fitting the total energy to 6th-order polynomial, the equilibrium bond length of 1.4169 Bohr is obtained.

ftot_H2_BL.png
↑

Optimizing the bond length (2) †

Alternatively, one can optimize the geometry (internal coordinate) by using the Hellmann-Feynman forces. The input file is as follows. Let's name it 'h2_relax.in.' Here we use the convergence threshold for the forces of 1.0 x 10-4 Ry/Bohr.

&control
   calculation   = 'relax'
   restart_mode  = 'from_scratch',
   pseudo_dir    =  '/home/ikutaro/QE/pseudo/'
   outdir        = './tmp/'
   prefix        = 'h2'
   tprnfor       = .true.
   forc_conv_thr = 1.d-4
/
&system
   ibrav   = 1
   A       = 10.d0
   nat     = 2
   ntyp    = 1
   nbnd    = 4
   ecutwfc = 60.0
   ecutrho = 240.0
/
&electrons
   diagonalization = 'david'
   conv_thr        = 1.0e-12
   mixing_beta     = 0.1
/
&ions
 ion_dynamics='bfgs'
/
ATOMIC_SPECIES
 H 0.0000  H_ONCV_PBE-1.0.upf
ATOMIC_POSITIONS (bohr)
H      0.000000000000      0.000000000000      0.00000000000
H      0.000000000000      0.000000000000      1.40000000000
K_POINTS (gamma)

The main differences from the SCF calculation are

   calculation   = 'relax'

and

&ions
 ion_dynamics='bfgs'
/

Here we use the BFGS algorithm for the structural optimization. Note the namelist &ions should be given even though the default parameters are used. In such a case

&ions
/

can be used. When the convergence for the structural relaxation is achieved, the final coordinates are given in the output file as

Begin final coordinates

ATOMIC_POSITIONS (bohr)
H        0.000000000   0.000000000  -0.008464243
H        0.000000000   0.000000000   1.408464243
End final coordinates

The bond length of 1.4169 Bohr obtained by the structural optimization by using the Hellmann-Feynman forces is in good agreement with that obtained by the manual structural optimization.

↑

Exercise †

The bond length also depends on the computational parameters such as cutoff energy and box size. Calculate the bond length as a function of cutoff energy and estimate the converged bond length.

トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS