![[PukiWiki]](image/logo_state-senri3_80x80.png "[PukiWiki]"){kind=logo}
第一原理分子動力学プログラム STATE Senri Wiki
- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- STATE_new_tutorial/Si_OPT_jp へ行く。
シリコン結晶 (セル最適化) †
ここでは結晶構造の最適化例としてシリコン結晶の平衡格子定数を求めましょう。 電子状態計算における最適化とは一般的には全エネルギーを最小化する電子の波動関数や構造を求めることを意味しており、エネルギーを最小化する格子定数を平衡格子定数と呼んでいます。 現在のワーキングディレクトリが~/STATE/examplesであるとして、Siディレクトリに移動します。
$ cd Si
ここでlsを実行し、nfで始まる入力ファイル群（nf*）や.shで終わるジョブスクリプト（*.sh）が含まれていることを確認します。
以下を実行して入力ファイルnfinp_scfを再確認しましょう。
$ cat nfinp_scf
#
# Crystalline silicon in the diamond structure
#
WF_OPT DAV
NTYP 1
NATM 2
TYPE 2
NSPG 227
GMAX 4.00
GMAXP 8.00
KPOINT_MESH 8 8 8
KPOINT_SHIFT OFF OFF OFF
WIDTH 0.0002
EDELTA 0.5000D-09
NEG 8
CELL 10.30 10.30 10.30 90.00 90.00 90.00
&ATOMIC_SPECIES
Si 28.0900 pot.Si_pbe1
&END
&ATOMIC_COORDINATES CRYSTAL
0.000000000000 0.000000000000 0.000000000000 1 1 1
0.250000000000 0.250000000000 0.250000000000 1 1 1
&END
同様にsb100で使用するジョブスクリプトqsub_sb100.shも確認しましょう。
$ cat qsub_sb100.sh
#$ -S /bin/sh
#$ -cwd
#$ -q sb.q
#$ -pe x6 6
#$ -N Si
module load intel/2021.2.0
module load intelmpi/2021.2.0
# Disable OPENMP parallelism
export OMP_NUM_THREADS=1
unset I_MPI_TCP_NETMASK
# Set the execuable of the STATE code
ln -fs ${HOME}/STATE/src/state-5.6.9/src/STATE .
# Set the pseudopotential data
ln -fs ../gncpp/pot.Si_pbe1
# Set the input/output file
INPUT_FILE=nfinp_scf
OUTPUT_FILE=nfout_scf
# Run!
mpirun ./STATE < ${INPUT_FILE} > ${OUTPUT_FILE}
結晶構造の最適化は以下のような手順で行います。
- 結晶の全エネルギーを体積の関数として計算
- エネルギー・体積（あるいは格子定数）曲線を状態方程式あるいは多項式にフィット
- エネルギーの最小値を与える体積（格子定数）を決定
エネルギーの最小値を与える体積（格子定数）を平衡体積（平衡格子定数）といいます。
ダイアモンド構造のシリコンは立方晶系に属し、単位胞に二つの原子を含み、格子定数はただ一つなので、ここでは格子定数Aのみを変化させます。
上でみた入力ファイルで格子定数を定義しているのは以下の行です。
CELL 10.30 10.30 10.30 90.00 90.00 90.00
ここで2-4コラムはBohr半径を単位とした格子定数A, B, Cを表し、5-7コラムは格子ベクトルA2とA3, A3とA1, A1とA2のなす角度（度）を表しています。
以下のようにA-Cを10.20から10.50まで0.05刻みで変えた入力ファイルを作成しましょう。
- 格子定数10.20用ファイルの準備
$ cp nfinp_scf nfinp_scf_10.20
- 格子定数10.20用ファイルの編集-格子定数の変更
CELL 10.20 10.20 10.20 90.00 90.00 90.00
- 格子定数10.25用ファイルの準備
$ cp nfinp_scf nfinp_scf_10.25
- 格子定数10.25用ファイルの編集-格子定数の変更
CELL 10.25 10.25 10.25 90.00 90.00 90.00
...
入力ファイルが準備できたらジョブスクリプト（qsub_sb100.sh）の以下の行を編集します。
# Set the input/output file INPUT_FILE=nfinp_scf OUTPUT_FILE=nfout_scf
- 格子定数10.20の場合
# Set the input/output file INPUT_FILE=nfinp_scf_10.20 OUTPUT_FILE=nfout_scf_10.20
- ジョブの投入
$ qsub qsub_sb100.sh
- 出力ファイル（nfout_scf_10.20）の確認
(これを10.50まで繰り返す)~
- ...
収束した全エネルギーは出力ファイルの以下の部分の
TOTAL ENERGY AND ITS COMPONENTS
TOTAL ENERGY = -7.87286120 A.U.
KINETIC ENERGY = 3.05638778 A.U.
HARTREE ENERGY = 0.53752775 A.U.
XC ENERGY = -2.41643958 A.U.
LOCAL ENERGY = -0.76652974 A.U.
NONLOCAL ENERGY = 0.16607187 A.U.
EWALD ENERGY = -8.44987928 A.U.
PC ENERGY = 0.00000000 A.U.
ENTROPIC ENERGY = 0.00000000 A.U.
TOTAL ENERGYの行にA.U./Hartreeで示されていますので、nfout_scf_10.20-10.50の全ての全エネルギーを取り出すと以下のようになります。
-7.87286120 -7.87332156 -7.87355833 -7.87364725 -7.87354557 -7.87325835 -7.87284975
格子定数の関数として表示すると以下のようになります。
10.20 -7.87286120 10.25 -7.87332156 10.30 -7.87355833 10.35 -7.87364725 10.40 -7.87354557 10.45 -7.87325835 10.50 -7.87284975
これをgnuplotで表示すると以下のようになります。
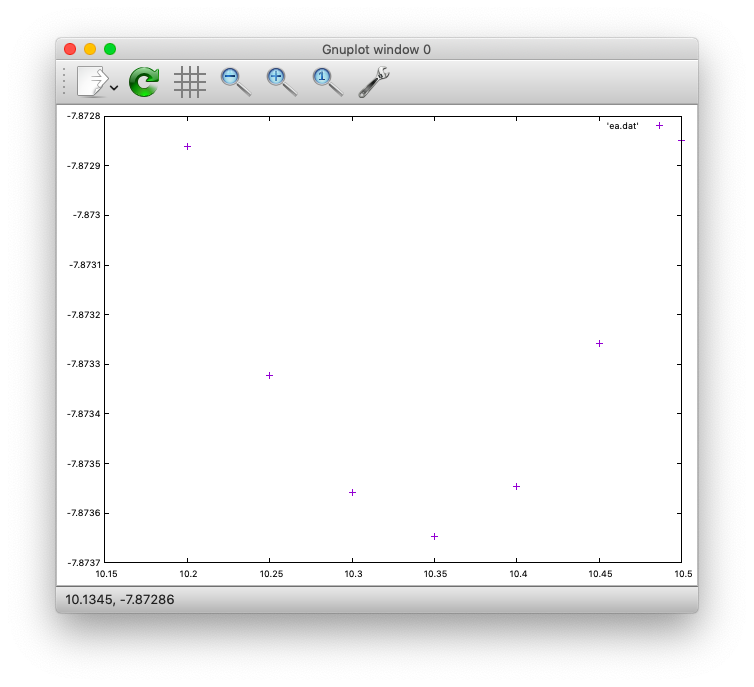
結晶の体積は出力ファイルの"PRIM. CELL VOLUME"に以下のように表示されています（Bohr半径の三乗）。
PRIM. CELL VOLUME : 0.265302E+03
この情報を使うと全エネルギーを体積の関数として以下のように表示することも可能です。
0.265302E+03 -7.87286120 0.269223E+03 -7.87332156 0.273182E+03 -7.87355833 0.277179E+03 -7.87364725 0.281216E+03 -7.87354557 0.285292E+03 -7.87325835 0.289406E+03 -7.87284975
データを取り出すのが面倒になったらstate2ev.shというユーティリティーを使ってみましょう。
$ state2ev.sh nfout_scf_*
出力データをetot.datというファイルに保存します。
$ state2ev.sh nfout_scf_* > etot.dat
これをgnuplotで表示します。
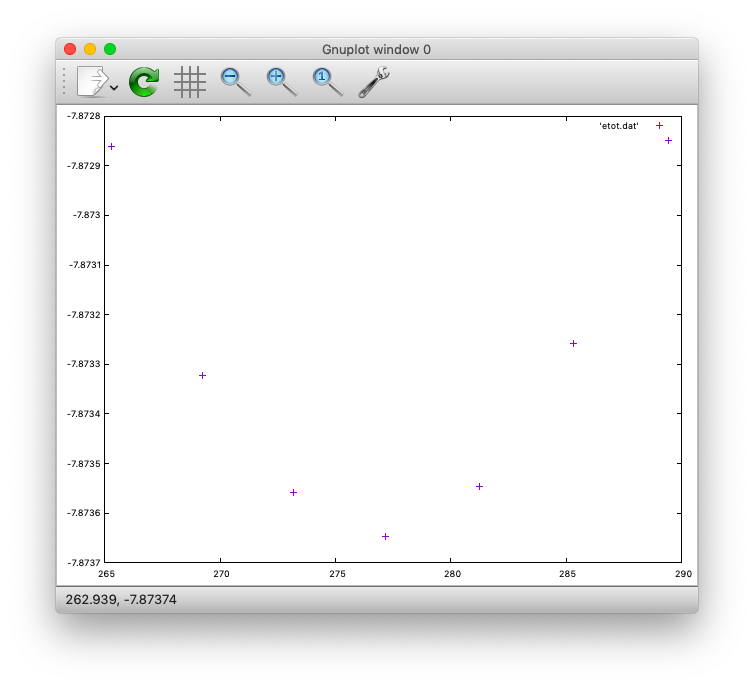
最後に得られたエネルギー・体積のデータをMurnaghan状態方程式にフィットします。ここではeosfitというユーティリティーを使いましょう。
$ eosfit etot.dat
これを実行するとフィットされたエネルギー・体積の曲線が以下のように表示されます。
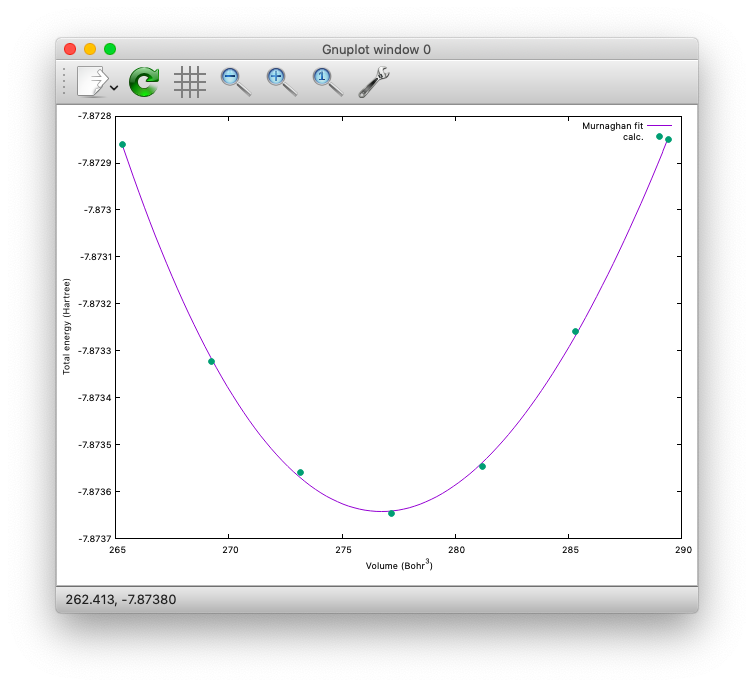
またフィッティングによって得られたパラメーターがeosfit.paramに出力されます。
eosfit.paramのv0が見積もられた平衡体積で、今の場合はV0=41.0085987716914 (Angstrom**3)が得られます（V0は平衡体積）。
平衡体積より平衡格子定数を求めると
a0=(4*V0)**(1/3) = 5.4741 (Angstrom)
が得られました。実験の格子定数と比較してみましょう。
